Закон ромба

(Статья)

Закон ромба – один из основных законов развития любой системы, он проявляется в случае, если наблюдать за развитием с помощью уровневой шкалы. Описан автором в работах по нелинейному уровневому подходу (НУП).

Если посмотреть на историю развития любой системы в уровневом разрезе – при продвижении её от подуровня к подуровню (от 0 к 1, или обратно), то можно увидеть определенную закономерность: динамика как бы раздваивается в средних, промежуточных областях уровневой шкалы, можно еще сказать утолщается, символизируя тем самым наибольшую противоречивость, непоследовательность, двойственность в отношениях между составляющими:

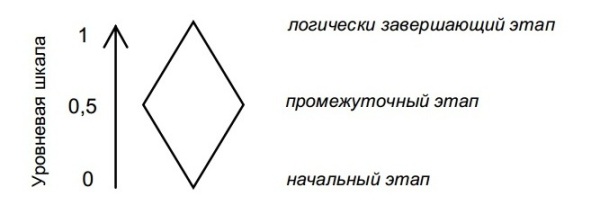
Изобразим ту же схему с учетом параметра времени (t):

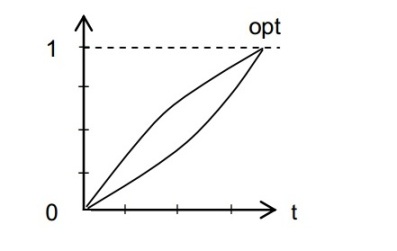
Вот это утолщение, на наш взгляд, иллюстрирует закон ромба.

На последнем рисунке изображен идеальный случай поведения динамики – система поступательно развивается от низшего к высшему, с возможным переходом на очередной уровень. В действительности так бывает не всегда, и схема развития процесса может быть представлена и следующим образом:

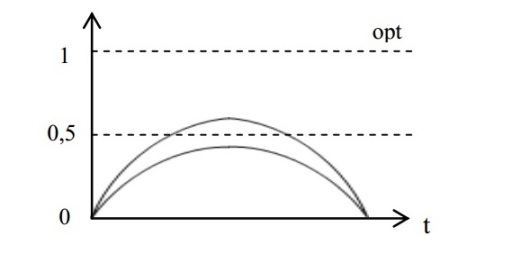
Существует много модификаций приведенных выше графиков – так, область утолщения может быть сильно вытянута вдоль пунктирной линии, соответствующей отметке 0,5, может «танцевать» вокруг неё, образуя колебания, динамика в целом может исходить из нуля, долго идти вдоль 0,5 и потом рвануть к единице, либо, наоборот, начать с единицы, задержаться на 0,5 и лишь впоследствии упасть до нуля и т.д. и т.п. Но во всех случаях мы будем иметь некий условный «ромб», который нужно лишь научиться видеть в многообразии графиков.

На взгляд автора, правило ромба чрезвычайно важно для понимания сути многих процессов в окружающем мире [1, 2, 3, 4]...

(ВНИМАНИЕ! Выше приведено начало статьи)

Скачать полный текст в формате PDF